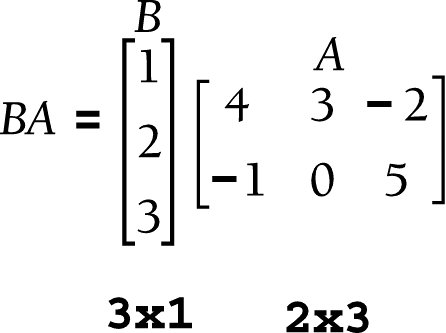11+ Matrix Multiplication Order Rules Gif

The matrix multiplication is also known as the matrix product or the multiplication of two matrices which will help in producing a single matrix. A good way to double check your work if you're multiplying matrices by hand is to confirm your answers with a matrix calculator. The rule for the multiplication of two matrices is the. matrix multiplication is different than multiplying a matrix using scalar multiplication. Distributivity associativity transpose reverses multiplication order solving a matrix equation warning properties of matrix arithmetic last time matrix multiplication violates one of the basic rules of traditional arithmetic:

In python, we can implement a matrix as nested list (list inside a list).

The answer matrix will have the dimensions of the outer dimensions as its final dimension. Implicit multiplication takes higher precedence than division. But the result of the product is different if we change the order of matrix. As the linked article notes, however, the required number of multiplications is different depending on which way the operation is performed. L = s * r * t. From the above two examples, we can observe the following for the matrix multiplication. S = local scale matrix. A × 0 = 0. And the product is d = abc. And this one will do a diagonal "flip" Yes, matrix multiplication results in a new matrix that composes the original functions. While there are many matrix calculators online, the simplest one to use that i have come across is this one by math is fun. When the transformation matrix a,b,c,d is the identity matrix (the matrix equivalent of "1") the x,y values are not changed:

2) matrix multiplication composes linear operations. Also, define a third matrix of size r2 rows and c1 columns. Implicit multiplication takes higher precedence than division. Ab can be found as follows. See how you understand this lesson.

matrix multiplication also has the distributive property, so:

Or "5×6 = 6×5"?that "rule" As the linked article notes, however, the required number of multiplications is different depending on which way the operation is performed. • given some matrices to multiply, determine the best order to multiply them so you minimize the number of single element multiplications. The matrix multiplication is done in the order srt, where s, r, and t are the matrices for scale, rotate, and translate, respectively. The matrix multiplication does not follow the commutative property. This fact is referred to as the associativity of matrix multiplication. We write this symbolically as: My current model is explained below: So with matrix algebra different rules apply than in the algebra of numbers. matrix multiplication is different than multiplying a matrix using scalar multiplication. matrix multiplication does not always commute. Vice versa • the transpose of a matrix is obtained by interchanging the rows and columns • if a and b have the same order: So intuitively , we can see that an implicit.

You can multiply matrices in excel thanks to the mmult function. Just as with addition and subtraction, multiplication and division share a set of rules, but the rules are different. A unit matrix of order 2 a unit matrix of order 3 01 0 ⎝ matrix multiplication unlike addition and subtraction, the order of two matrices need not be the same for multiplication. Goal what familiar properties does matrix arithmetic have? The order of a matrix is number of rows *number of columns.

Point out to students that there are a few general rules of matrix multiplication that are useful to know, including:

Point out to students that there are a few general rules of matrix multiplication that are useful to know, including: We can treat each element as a row of the matrix. matrix multiplication is a simple binary operation that produces a single matrix from the entries of two given matrices. The syntax for the function is: So for 6 / 2 (1+2) is 6 / 2*(1+2). Implementation of addition,subtraction and multiplication of matrix in c++ programming language. This is my first post here, so if i unknowingly vioated any rules, mods are welcome to edit my post accordingly. The matrix multiplication is also known as the matrix product or the multiplication of two matrices which will help in producing a single matrix. As the linked article notes, however, the required number of multiplications is different depending on which way the operation is performed. Of columns as matrix b. In multiplying matrices, it helps to remember this key rule: Equality addition multiplication special matrices if a = b and a = c,. The matrix multiplication is done in the order srt, where s, r, and t are the matrices for scale, rotate, and translate, respectively.

11+ Matrix Multiplication Order Rules Gif. A good way to double check your work if you're multiplying matrices by hand is to confirm your answers with a matrix calculator. matrix multiplication with the mmult excel function. The product of matrices is not commutative, that is, the result of multiplying two matrices depends on the order in which they are multiplied: It is important to recognize that the power of a matrix is only well defined if the matrix is a square matrix. Probably seemed fairly stupid at the time, because you already knew that order didn't matter in multiplication.