Most familiar as the name of the property that says "3 + 4 = 4 + 3"
Addition, subtraction, multiplication, and division. Closure/totality (any two elements of the group can be multiplied to get another element of the group), associativity, ident. In other words, no matter how we parenthesize the product, the result will be the same. If you swap the two matrices, you're swapping which one contributes rows and which one contributes columns to the result. Or "5×6 = 6×5"?that "rule"

matrix multiplication matrix multiplication is an operation with properties quite different from its scalar counterpart.
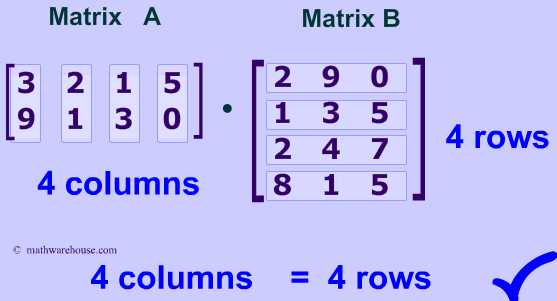
The key to answering this question is to look at the dimensions of each matrix. The required axioms matrix multiplication must satisfy to be a group operation (the operation is not the whole group) are: In other words, if you have a matrix called a, and a matrix called b, then a∙b≠b∙a (the 'dot' Overview matrices are a way of grouping numbers, and are organized into rows and columns. For instance, in our example of multiplication of 3 matrices d = abc, it doesn't matter if we perform ab first or bc first. First, consider expressions that include one or more of the arithmetic operations: At the level of arithmetic, the order matters because matrix multiplication involves combining the rows of the first matrix with the columns of the second. Simply put, a matrix is an array of numbers with a predefined number of rows and colums. order doesn't matter when a matrix is multiplied with its inverse. matrix multiplication is not cumulative, so the order of matrices matters. So, in general, you should assume that they are not equal. If you swap the two matrices, you're swapping which one contributes rows and which one contributes columns to the result. In 3d graphics we will mostly use 4x4 matrices.
A typical world transformation matrix is shown in the following example. Properties of multiplication do not hold, many more do. For example, the polar form vector…. What makes a matrix commutative? Or "2 × 5 = 5 × 2", the property can also be used in more advanced settings.

We can multiply two vectors using numpy.dot() method.
There is one particular matrix, the identity matrix, which has very So, in general, you should assume that they are not equal. So the order that c++ calls operators in just doesn't matter for matrix multiplication. The order of the multiplication does not matter in this case: This lecture introduces matrix multiplication,. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. When matrix multiplication is defined, multiplication by the unit matrix leaves the original matrix unchanged. Simply put, a matrix is an array of numbers with a predefined number of rows and colums. The order of the factors matters. So matrix multiplication, you have to be very careful about keeping things in the same order as you're multiplying. matrix multiplication was first defined explicitly in print by cayley in. Because multiplication of square matrices is common, it is helpful to point out a. If the product of two symmetric matrices is symmetric, then they must commute.
At the level of arithmetic, the order matters because matrix multiplication involves combining the rows of the first matrix with the columns of the second. This is what the calculation should have been. multiplication of matrices is not commutative but when we multiply a matrix with its inverse multiplication can be commutative. The issue was with the order in which i was multiplying the translation matrix and the vector. So the order that c++ calls operators in just doesn't matter for matrix multiplication.

Multiplying a scalar constant across matrix multiplication is commutative in the following form;
With multiplication, ordering also matters The formulas are not intuitive, but it's nothing other than the simple idea of combining two linear changes of variables in succession. In other words, no matter how we parenthesize the product, the result will be the same. But (a * (b * c)) is the same as ((a * b) * c), for both matrix and scalar multiplication. Let us do an example in python. At the level of arithmetic, the order matters because matrix multiplication involves combining the rows of the first matrix with the columns of the second. At the level of arithmetic, the order matters because matrix multiplication involves combining the rows of the first matrix with the columns of the second. In 3d graphics we will mostly use 4x4 matrices. The identity matrix is a special matrix and the order of multiplication does not matter as shown above. Or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. You can't switch the order and get the same result. That is, the matrix product ab need not be the same as the matrix product ba. (a / (b / c)) is not the same as ((a / b) / c).
Get Matrix Multiplication Order Matters Background. We have many options to multiply a chain of matrices because matrix multiplication is associative. Closure/totality (any two elements of the group can be multiplied to get another element of the group), associativity, ident. The scalar changes the size of the vector. The key to answering this question is to look at the dimensions of each matrix. It is important to memorize that the original dimensions of the matrix are the same after the scalar multiplication.
matrix multiplication is not commutative: matrix multiplication order. Just like any number multiplied by 1 gives the same number, the same is true for any matrix multiplied with the identity matrix.